引言
最近在面试中,除了基础 & 算法 & 项目之外,经常被问到或被要求介绍和描述下自己所知道的几种分类或聚类算法(当然,这完全不代表你将来的面试中会遇到此类问题,只是因为我的简历上写了句:熟悉常见的聚类 & 分类算法而已),而我向来恨对一个东西只知其皮毛而不得深入,故写一个有关数据挖掘十大算法的系列文章以作为自己备试之用,甚至以备将来常常回顾思考。行文杂乱,但侥幸若能对读者起到一点帮助,则幸甚至哉。
本文借鉴和参考了两本书,一本是Tom M.Mitchhell所著的机器学习,一本是数据挖掘导论,这两本书皆分别是机器学习 & 数据挖掘领域的开山 or 杠鼎之作,读者有继续深入下去的兴趣的话,不妨在阅读本文之后,课后细细研读这两本书。除此之外,还参考了网上不少牛人的作品(文末已注明参考文献或链接),在此,皆一一表示感谢(从本质上来讲,本文更像是一篇读书 & 备忘笔记)。
说白了,一年多以前,我在本blog内写过一篇文章,叫做:数据挖掘领域十大经典算法初探(题外话:最初有个出版社的朋友便是因此文找到的我,尽管现在看来,我离出书日期仍是遥遥无期)。现在,我抽取其中几个最值得一写的几个算法每一个都写一遍,以期对其有个大致通透的了解。
OK,暂称本系列为Top 10 Algorithms in Data Mining,若全系列任何一篇文章若有任何错误,漏洞,或不妥之处,还请读者们一定要随时不吝赐教 & 指正,谢谢各位。
分类与聚类,监督学习与无监督学习
在讲具体的分类和聚类算法之前,有必要讲一下什么是分类,什么是聚类,以及都包含哪些具体算法或问题。
- Classification (分类),对于一个 classifier ,通常需要你告诉它“这个东西被分为某某类”这样一些例子,理想情况下,一个 classifier 会从它得到的训练集中进行“学习”,从而具备对未知数据进行分类的能力,这种提供训练数据的过程通常叫做 supervised learning (监督学习),
- 而Clustering(聚类),简单地说就是把相似的东西分到一组,聚类的时候,我们并不关心某一类是什么,我们需要实现的目标只是把相似的东西聚到一起,因此,一个聚类算法通常只需要知道如何计算相似 度就可以开始工作了,因此 clustering 通常并不需要使用训练数据进行学习,这在 Machine Learning 中被称作 unsupervised learning (无监督学习).
常见的分类与聚类算法
所谓分类分类,简单来说,就是根据文本的特征或属性,划分到已有的类别中。如在自然语言处理NLP中,我们经常提到的文本分类便就是一个分类问题,一般的模式分类方法都可用于文本分类研究。常用的分类算法包括:决策树分类法,朴素的贝叶斯分类算法(native Bayesian classifier)、基于支持向量机(SVM)的分类器,神经网络法,k-最近邻法(k-nearest neighbor,kNN),模糊分类法等等(所有这些分类算法日后在本blog内都会一一陆续阐述)。
分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应。但是很多时候上述条件得不到满足,尤其是在处理海量数据的时候,如果通过预处理使得数据满足分类算法的要求,则代价非常大,这时候可以考虑使用聚类算法。
而K均值(K-means clustering)聚类则是最典型的聚类算法(当然,除此之外,还有很多诸如属于划分法K-MEDOIDS算法、CLARANS算法;属于层次法的BIRCH算法、CURE算法、CHAMELEON算法等;基于密度的方法:DBSCAN算法、OPTICS算法、DENCLUE算法等;基于网格的方法:STING算法、CLIQUE算法、WAVE-CLUSTER算法;基于模型的方法,本系列后续会介绍其中几种)。
监督学习与无监督学习
机器学习发展到现在,一般划分为 监督学习(supervised learning),半监督学习(semi-supervised learning)以及无监督学习(unsupervised learning)三类。举个具体的对应例子,则是比如说,在NLP词义消岐中,也分为监督的消岐方法,和无监督的消岐方法。在有监督的消岐方法中,训练数据是已知的,即每个词的语义分类是被标注了的;而在无监督的消岐方法中,训练数据是未经标注的。
上面所介绍的常见的分类算法属于监督学习,聚类则属于无监督学习(反过来说,监督学习属于分类算法则不准确,因为监督学习只是说我们给样本sample同时打上了标签(label),然后同时利用样本和标签进行相应的学习任务,而不是仅仅局限于分类任务。常见的其他监督问题,比如相似性学习,特征学习等等也是监督的,但是不是分类)。
再举个例子,正如人们通过已知病例学习诊断技术那样,计算机要通过学习才能具有识别各种事物和现象的能力。用来进行学习的材料就是与被识别对象属于同类的有限数量样本。监督学习中在给予计算机学习样本的同时,还告诉计算各个样本所属的类别。若所给的学习样本不带有类别信息,就是无监督学习(浅显点说:同样是学习训练,监督学习中,给的样例比如是已经标注了如心脏病的,肝炎的;而无监督学习中,就是给你一大堆的样例,没有标明是何种病例的)。
而在支持向量机导论一书给监督学习下的定义是:当样例是输入/输出对给出时,称为监督学习,有关输入/输出函数关系的样例称为训练数据。而在无监督学习中,其数据不包含输出值,学习的任务是理解数据产生的过程。
第一部分、决策树学习
1.1、什么是决策树
咱们直接切入正题。所谓决策树,顾名思义,是一种树,一种依托于策略抉择而建立起来的树。
机器学习中,决策树是一个预测模型;他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。
从数据产生决策树的机器学习技术叫做决策树学习, 通俗点说就是决策树,说白了,这是一种依托于分类、训练上的预测树,根据已知预测、归类未来。
来理论的太过抽象,下面举两个浅显易懂的例子:
第一个例子
套用俗语,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑:
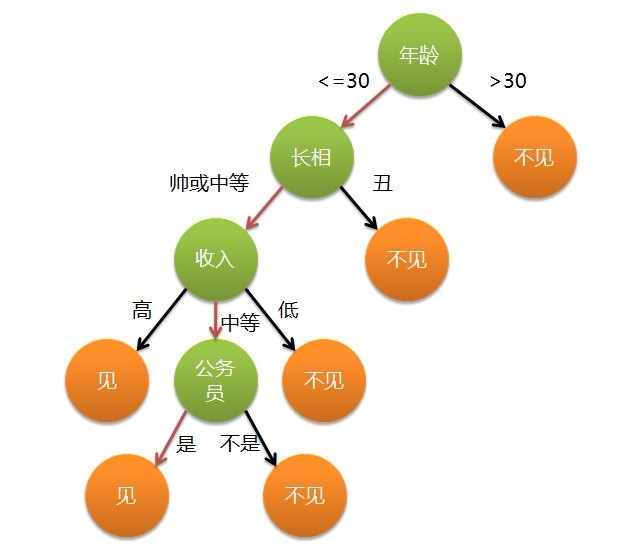
也就是说,决策树的简单策略就是,好比公司招聘面试过程中筛选一个人的简历,如果你的条件相当好比如说某985/211重点大学博士毕业,那么二话不说,直接叫过来面试,如果非重点大学毕业,但实际项目经验丰富,那么也要考虑叫过来面试一下,即所谓具体情况具体分析、决策。但每一个未知的选项都是可以归类到已有的分类类别中的。
第二个例子
此例子来自Tom M.Mitchell著的机器学习一书:
小王的目的是通过下周天气预报寻找什么时候人们会打高尔夫,他了解到人们决定是否打球的原因最主要取决于天气情况。而天气状况有晴,云和雨;气温用华氏温度表示;相对湿度用百分比;还有有无风。如此,我们便可以构造一棵决策树,如下(根据天气这个分类决策这天是否合适打网球):
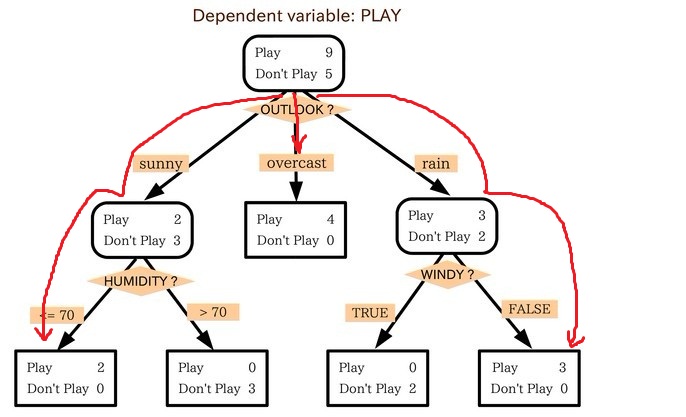
上述决策树对应于以下表达式:
(Outlook=Sunny ^Humidity<=70)V (Outlook = Overcast)V (Outlook=Rain ^ Wind=Weak)
1.2、ID3算法
1.2.1、决策树学习之ID3算法
ID3算法是决策树算法的一种。想了解什么是ID3算法之前,我们得先明白一个概念:奥卡姆剃刀。
- 奥卡姆剃刀(Occam’s Razor, Ockham’s Razor),又称“奥坎的剃刀”,是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉(William of Occam,约1285年至1349年)提出,他在《箴言书注》2卷15题说“切勿浪费较多东西,去做‘用较少的东西,同样可以做好的事情’。简单点说,便是:be simple。
ID3算法(Iterative Dichotomiser 3 迭代二叉树3代)是一个由Ross Quinlan发明的用于决策树的算法。这个算法便是建立在上述所介绍的奥卡姆剃刀的基础上:越是小型的决策树越优于大的决策树(be simple简单理论)。尽管如此,该算法也不是总是生成最小的树形结构,而是一个启发式算法。
OK,从信息论知识中我们知道,期望信息越小,信息增益越大,从而纯度越高。ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益(很快,由下文你就会知道信息增益又是怎么一回事)最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策树空间。
所以,ID3的思想便是:
- 自顶向下的贪婪搜索遍历可能的决策树空间构造决策树(此方法是ID3算法和C4.5算法的基础);
- 从“哪一个属性将在树的根节点被测试”开始;
- 使用统计测试来确定每一个实例属性单独分类训练样例的能力,分类能力最好的属性作为树的根结点测试(如何定义或者评判一个属性是分类能力最好的呢?这便是下文将要介绍的信息增益,or 信息增益率)。
- 然后为根结点属性的每个可能值产生一个分支,并把训练样例排列到适当的分支(也就是说,样例的该属性值对应的分支)之下。
重复这个过程,用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。
这形成了对合格决策树的贪婪搜索,也就是算法从不回溯重新考虑以前的选择。
下图所示即是用于学习布尔函数的ID3算法概要:

1.2.2、哪个属性是最佳的分类属性
1、信息增益的度量标准:熵
上文中,我们提到:“ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益(很快,由下文你就会知道信息增益又是怎么一回事)最大的属性进行分裂。”接下来,咱们就来看看这个信息增益是个什么概念(当然,在了解信息增益之前,你必须先理解:信息增益的度量标准:熵)。
上述的ID3算法的核心问题是选取在树的每个结点要测试的属性。我们希望选择的是最有利于分类实例的属性,信息增益(Information Gain)是用来衡量给定的属性区分训练样例的能力,而ID3算法在增长树的每一步使用信息增益从候选属性中选择属性。
为了精确地定义信息增益,我们先定义信息论中广泛使用的一个度量标准,称为熵(entropy),它刻画了任意样例集的纯度(purity)。给定包含关于某个目标概念的正反样例的样例集S,那么S相对这个布尔型分类的熵为:
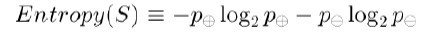
上述公式中,p+代表正样例,比如在本文开头第二个例子中p+则意味着去打羽毛球,而p-则代表反样例,不去打球(在有关熵的所有计算中我们定义0log0为0)。
如果写代码实现熵的计算,则如下所示:
1 | //根据具体属性和值来计算熵 |
1.3.3、C4.5算法实现中的几个关键步骤
在上文中,我们已经知道了决策树学习C4.5算法中4个重要概念的表达,如下:
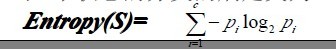
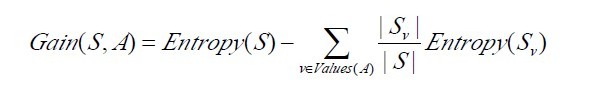
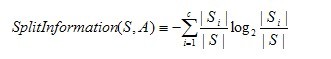
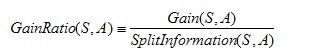
接下来,咱们写下代码实现,
1、信息熵
1 | double C4_5::entropy(int *attrClassCount, int classNum, int allNum){ |
2、信息增益率
1 | double C4_5::gainRatio(int classNum, vector<int *> attriCount, double pEntropy){ |
3、选取最大增益属性作为分类条件
1 | int C4_5::chooseAttribute(vector<int> attrIndex, vector<int *>* sampleCount){ |
1.4、读者点评
- form Wind:决策树使用于特征取值离散的情况,连续的特征一般也要处理成离散的(而很多文章没有表达出决策树的关键特征or概念)。实际应用中,决策树overfitting比较的严重,一般要做boosting。分类器的性能上不去,很主要的原因在于特征的鉴别性不足,而不是分类器的好坏,好的特征才有好的分类效果,分类器只是弱相关。
- 那如何提高 特征的鉴别性呢?一是设计特征时尽量引入domain knowledge,二是对提取出来的特征做选择、变换和再学习,这一点是机器学习算法不管的部分(我说的这些不是针对决策树的,因此不能说是决策树的特点,只是一些机器学习算法在应用过程中的经验体会)。
第二部分、贝叶斯分类
插播:关于贝叶斯方法,更清晰简洁的论述请见此文第一部分:从贝叶斯方法谈到贝叶斯网络。July、2014年11月14日更新。
关于贝叶斯,有篇文章介绍的不错:数学之美番外篇:平凡而又神奇的贝叶斯方法,本文第二部分之大部分基本整理自未鹏兄之手(做了部分改动),若有任何不妥之处,还望原作者和众读者海涵,谢谢(当然,日后找机会会重新贝叶斯。PS:后续已经重写,见此文第一部分)。
2.1、什么是贝叶斯分类
据维基百科上的介绍,贝叶斯定理是关于随机事件A和B的条件概率和边缘概率的一则定理。

如上所示,其中P(A|B)是在B发生的情况下A发生的可能性。在贝叶斯定理中,每个名词都有约定俗成的名称:
- P(A)是A的先验概率或边缘概率。之所以称为”先验”是因為它不考虑任何B方面的因素。
- P(A|B)是已知B发生后A的条件概率(直白来讲,就是先有B而后=>才有A),也由于得自B的取值而被称作A的后验概率。
- P(B|A)是已知A发生后B的条件概率(直白来讲,就是先有A而后=>才有B),也由于得自A的取值而被称作B的后验概率。
- P(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
按这些术语,Bayes定理可表述为:后验概率 = (相似度*先验概率)/标准化常量,也就是說,后验概率与先验概率和相似度的乘积成正比。另外,比例P(B|A)/P(B)也有时被称作标准相似度(standardised likelihood),Bayes定理可表述为:后验概率 = 标准相似度*先验概率。
2.2 贝叶斯公式如何而来
贝叶斯公式是怎么来的?下面再举wikipedia 上的一个例子:
一所学校里面有 60% 的男生,40% 的女生。男生总是穿长裤,女生则一半穿长裤一半穿裙子。有了这些信息之后我们可以容易地计算“随机选取一个学生,他(她)穿长裤的概率和穿裙子的概率是多大”,这个就是前面说的“正向概率”的计算。然而,假设你走在校园中,迎面走来一个穿长裤的学生(很不幸的是你高度近似,你只看得见他(她)穿的是否长裤,而无法确定他(她)的性别),你能够推断出他(她)是男生的概率是多大吗?
一些认知科学的研究表明(《决策与判断》以及《Rationality for Mortals》第12章:小孩也可以解决贝叶斯问题),我们对形式化的贝叶斯问题不擅长,但对于以频率形式呈现的等价问题却很擅长。在这里,我们不妨把问题重新叙述成:你在校园里面随机游走,遇到了 N 个穿长裤的人(仍然假设你无法直接观察到他们的性别),问这 N 个人里面有多少个女生多少个男生。
你说,这还不简单:算出学校里面有多少穿长裤的,然后在这些人里面再算出有多少女生,不就行了?
我们来算一算:假设学校里面人的总数是 U 个。60% 的男生都穿长裤,于是我们得到了 U * P(Boy) * P(Pants|Boy) 个穿长裤的(男生)(其中 P(Boy) 是男生的概率 = 60%,这里可以简单的理解为男生的比例;P(Pants|Boy) 是条件概率,即在 Boy 这个条件下穿长裤的概率是多大,这里是 100% ,因为所有男生都穿长裤)。40% 的女生里面又有一半(50%)是穿长裤的,于是我们又得到了 U * P(Girl) * P(Pants|Girl) 个穿长裤的(女生)。加起来一共是 U * P(Boy) * P(Pants|Boy) + U* P(Girl) * P(Pants|Girl) 个穿长裤的,其中有 U * P(Girl) * P(Pants|Girl) 个女生。两者一比就是你要求的答案。
下面我们把这个答案形式化一下:我们要求的是 P(Girl|Pants) (穿长裤的人里面有多少女生),我们计算的结果是 U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)] 。容易发现这里校园内人的总数是无关的,两边同时消去U,于是得到
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
注意,如果把上式收缩起来,分母其实就是 P(Pants) ,分子其实就是 P(Pants, Girl) 。而这个比例很自然地就读作:在穿长裤的人( P(Pants) )里面有多少(穿长裤)的女孩( P(Pants, Girl) )。
上式中的 Pants 和 Boy/Girl 可以指代一切东西,So,其一般形式就是:
P(B|A) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]
收缩起来就是:
P(B|A) = P(AB) / P(A)
其实这个就等于:P(B|A) * P(A) = P(AB)
更进一步阐述,P(B|A)便是在条件A的情况下,B出现的概率是多大。然看似这么平凡的贝叶斯公式,背后却隐含着非常深刻的原理。
2.3、拼写纠正
经典著作《人工智能:现代方法》的作者之一 Peter Norvig 曾经写过一篇介绍如何写一个拼写检查/纠正器的文章,里面用到的就是贝叶斯方法,下面,将其核心思想简单描述下。
首先,我们需要询问的是:“问题是什么?”
问题是我们看到用户输入了一个不在字典中的单词,我们需要去猜测:“这个家伙到底真正想输入的单词是什么呢?”用刚才我们形式化的语言来叙述就是,我们需要求:
P(我们猜测他想输入的单词 | 他实际输入的单词)
这个概率。并找出那个使得这个概率最大的猜测单词。显然,我们的猜测未必是唯一的,就像前面举的那个自然语言的歧义性的例子一样;这里,比如用户输入: thew ,那么他到底是想输入 the ,还是想输入 thaw ?到底哪个猜测可能性更大呢?幸运的是我们可以用贝叶斯公式来直接出它们各自的概率,我们不妨将我们的多个猜测记为 h1 h2 .. ( h 代表 hypothesis),它们都属于一个有限且离散的猜测空间 H (单词总共就那么多而已),将用户实际输入的单词记为 D ( D 代表 Data ,即观测数据),于是
P(我们的猜测1 | 他实际输入的单词)
可以抽象地记为:
P(h1 | D)
类似地,对于我们的猜测2,则是 P(h2 | D)。不妨统一记为:
P(h | D)
运用一次贝叶斯公式,我们得到:
P(h | D) = P(h) * P(D | h) / P(D)
对于不同的具体猜测 h1 h2 h3 .. ,P(D) 都是一样的,所以在比较 P(h1 | D) 和 P(h2 | D) 的时候我们可以忽略这个常数。即我们只需要知道:
P(h | D) ∝ P(h) * P(D | h) (注:那个符号的意思是“正比例于”,不是无穷大,注意符号右端是有一个小缺口的。)
这个式子的抽象含义是:对于给定观测数据,一个猜测是好是坏,取决于“这个猜测本身独立的可能性大小(先验概率,Prior )”和“这个猜测生成我们观测到的数据的可能性大小”(似然,Likelihood )的乘积。具体到我们的那个 thew 例子上,含义就是,用户实际是想输入 the 的可能性大小取决于 the 本身在词汇表中被使用的可能性(频繁程度)大小(先验概率)和 想打 the 却打成 thew 的可能性大小(似然)的乘积。
剩下的事情就很简单了,对于我们猜测为可能的每个单词计算一下 P(h) * P(D | h) 这个值,然后取最大的,得到的就是最靠谱的猜测。更多细节请参看未鹏兄之原文。
2.4、贝叶斯的应用
2.4.1、中文分词
贝叶斯是机器学习的核心方法之一。比如中文分词领域就用到了贝叶斯。浪潮之巅的作者吴军在《数学之美》系列中就有一篇是介绍中文分词的。这里介绍一下核心的思想,不做赘述,详细请参考吴军的原文。
分词问题的描述为:给定一个句子(字串),如:
南京市长江大桥
如何对这个句子进行分词(词串)才是最靠谱的。例如:
1.南京市/长江大桥
2.南京/市长/江大桥
这两个分词,到底哪个更靠谱呢?
我们用贝叶斯公式来形式化地描述这个问题,令 X 为字串(句子),Y 为词串(一种特定的分词假设)。我们就是需要寻找使得 P(Y|X) 最大的 Y ,使用一次贝叶斯可得:
P(Y|X) ∝ P(Y)*P(X|Y)
用自然语言来说就是 这种分词方式(词串)的可能性 乘以 这个词串生成我们的句子的可能性。我们进一步容易看到:可以近似地将 P(X|Y) 看作是恒等于 1 的,因为任意假想的一种分词方式之下生成我们的句子总是精准地生成的(只需把分词之间的分界符号扔掉即可)。于是,我们就变成了去最大化 P(Y) ,也就是寻找一种分词使得这个词串(句子)的概率最大化。而如何计算一个词串:
W1, W2, W3, W4 ..
的可能性呢?我们知道,根据联合概率的公式展开:P(W1, W2, W3, W4 ..) = P(W1) P(W2|W1) P(W3|W2, W1) P(W4|W1,W2,W3) .. 于是我们可以通过一系列的条件概率(右式)的乘积来求整个联合概率。然而不幸的是随着条件数目的增加(P(Wn|Wn-1,Wn-2,..,W1) 的条件有 n-1 个),数据稀疏问题也会越来越严重,即便语料库再大也无法统计出一个靠谱的 P(Wn|Wn-1,Wn-2,..,W1) 来。为了缓解这个问题,计算机科学家们一如既往地使用了“天真”假设:我们假设句子中一个词的出现概率只依赖于它前面的有限的 k 个词(k 一般不超过 3,如果只依赖于前面的一个词,就是2元语言模型(2-gram),同理有 3-gram 、 4-gram 等),这个就是所谓的“有限地平线”假设。
虽然上面这个假设很傻很天真,但结果却表明它的结果往往是很好很强大的,后面要提到的朴素贝叶斯方法使用的假设跟这个精神上是完全一致的,我们会解释为什么像这样一个天真的假设能够得到强大的结果。目前我们只要知道,有了这个假设,刚才那个乘积就可以改写成: P(W1) P(W2|W1) P(W3|W2) * P(W4|W3) .. (假设每个词只依赖于它前面的一个词)。而统计 P(W2|W1) 就不再受到数据稀疏问题的困扰了。对于我们上面提到的例子“南京市长江大桥”,如果按照自左到右的贪婪方法分词的话,结果就成了“南京市长/江大桥”。但如果按照贝叶斯分词的话(假设使用 3-gram),由于“南京市长”和“江大桥”在语料库中一起出现的频率为 0 ,这个整句的概率便会被判定为 0 。 从而使得“南京市/长江大桥”这一分词方式胜出。
2.4.2、贝叶斯图像识别,Analysis by Synthesis
贝叶斯方法是一个非常 general 的推理框架。其核心理念可以描述成:Analysis by Synthesis (通过合成来分析)。06 年的认知科学新进展上有一篇 paper 就是讲用贝叶斯推理来解释视觉识别的,一图胜千言,下图就是摘自这篇 paper :

首先是视觉系统提取图形的边角特征,然后使用这些特征自底向上地激活高层的抽象概念(比如是 E 还是 F 还是等号),然后使用一个自顶向下的验证来比较到底哪个概念最佳地解释了观察到的图像。
2.4.3、最大似然与最小二乘

学过线性代数的大概都知道经典的最小二乘方法来做线性回归。问题描述是:给定平面上 N 个点,(这里不妨假设我们想用一条直线来拟合这些点——回归可以看作是拟合的特例,即允许误差的拟合),找出一条最佳描述了这些点的直线。
一个接踵而来的问题就是,我们如何定义最佳?我们设每个点的坐标为 (Xi, Yi) 。如果直线为 y = f(x) 。那么 (Xi, Yi) 跟直线对这个点的“预测”:(Xi, f(Xi)) 就相差了一个 ΔYi = |Yi – f(Xi)| 。最小二乘就是说寻找直线使得 (ΔY1)^2 + (ΔY2)^2 + .. (即误差的平方和)最小,至于为什么是误差的平方和而不是误差的绝对值和,统计学上也没有什么好的解释。然而贝叶斯方法却能对此提供一个完美的解释。
我们假设直线对于坐标 Xi 给出的预测 f(Xi) 是最靠谱的预测,所有纵坐标偏离 f(Xi) 的那些数据点都含有噪音,是噪音使得它们偏离了完美的一条直线,一个合理的假设就是偏离路线越远的概率越小,具体小多少,可以用一个正态分布曲线来模拟,这个分布曲线以直线对 Xi 给出的预测 f(Xi) 为中心,实际纵坐标为 Yi 的点 (Xi, Yi) 发生的概率就正比于 EXP[-(ΔYi)^2]。(EXP(..) 代表以常数 e 为底的多少次方)。
现在我们回到问题的贝叶斯方面,我们要想最大化的后验概率是:
P(h|D) ∝ P(h) * P(D|h)
又见贝叶斯!这里 h 就是指一条特定的直线,D 就是指这 N 个数据点。我们需要寻找一条直线 h 使得 P(h) * P(D|h) 最大。很显然,P(h) 这个先验概率是均匀的,因为哪条直线也不比另一条更优越。所以我们只需要看 P(D|h) 这一项,这一项是指这条直线生成这些数据点的概率,刚才说过了,生成数据点 (Xi, Yi) 的概率为 EXP[-(ΔYi)^2] 乘以一个常数。而 P(D|h) = P(d1|h) * P(d2|h) * .. 即假设各个数据点是独立生成的,所以可以把每个概率乘起来。于是生成 N 个数据点的概率为 EXP[-(ΔY1)^2] * EXP[-(ΔY2)^2] * EXP[-(ΔY3)^2] * .. = EXP{-[(ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + ..]} 最大化这个概率就是要最小化 (ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + .. 。 熟悉这个式子吗?
除了以上所介绍的之外,贝叶斯还在词义消岐,语言模型的平滑方法中都有一定应用。下节,咱们再来简单看下朴素贝叶斯方法。
2.5、朴素贝叶斯方法
朴素贝叶斯方法是一个很特别的方法,所以值得介绍一下。在众多的分类模型中,应用最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model,NBC)。 朴素贝叶斯模型发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。
同时,NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,这给NBC模型的正确分类带来了一定影响。在属性个数比较多或者属性之间相关性较大时,NBC模型的分类效率比不上决策树模型。而在属性相关性较小时,NBC模型的性能最为良好。
接下来,我们用朴素贝叶斯在垃圾邮件过滤中的应用来举例说明。
2.5.1、贝叶斯垃圾邮件过滤器
问题是什么?问题是,给定一封邮件,判定它是否属于垃圾邮件。按照先例,我们还是用 D 来表示这封邮件,注意 D 由 N 个单词组成。我们用 h+ 来表示垃圾邮件,h- 表示正常邮件。问题可以形式化地描述为求:
1 | P(h+|D) = P(h+) * P(D|h+) / P(D) |
private static String lineProcess(String line, ArrayList<String> stopWordsArray) throws IOException {
// TODO Auto-generated method stub
//step1 英文词法分析,去除数字、连字符、标点符号、特殊字符,所有大写字母转换成小写,可以考虑用正则表达式
String res[] = line.split("[^a-zA-Z]");
//这里要小心,防止把有单词中间有数字和连字符的单词 截断了,但是截断也没事
String resString = new String();
//step2去停用词
//step3stemming,返回后一起做
for(int i = 0; i < res.length; i++){
if(!res[i].isEmpty() && !stopWordsArray.contains(res[i].toLowerCase())){
resString += " " + res[i].toLowerCase() + " ";
}
}
return resString;
}
1 |
|
package com.pku.yangliu;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;
import java.math.BigDecimal;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
import java.util.SortedSet;
import java.util.TreeMap;
import java.util.TreeSet;
import java.util.Vector;
/**利用朴素贝叶斯算法对newsgroup文档集做分类,采用十组交叉测试取平均值
* 采用多项式模型,stanford信息检索导论课件上面言多项式模型比伯努利模型准确度高
* 类条件概率P(tk|c)=(类c 下单词tk 在各个文档中出现过的次数之和+1)/(类c下单词总数+|V|)
*/
public class NaiveBayesianClassifier {
/**用贝叶斯法对测试文档集分类
* @param trainDir 训练文档集目录
* @param testDir 测试文档集目录
* @param classifyResultFileNew 分类结果文件路径
* @throws Exception
*/
private void doProcess(String trainDir, String testDir,
String classifyResultFileNew) throws Exception {
// TODO Auto-generated method stub
Map<String,Double> cateWordsNum = new TreeMap<String,Double>();//保存训练集每个类别的总词数
Map<String,Double> cateWordsProb = new TreeMap<String,Double>();//保存训练样本每个类别中每个属性词的出现词数
cateWordsProb = getCateWordsProb(trainDir);
cateWordsNum = getCateWordsNum(trainDir);
double totalWordsNum = 0.0;//记录所有训练集的总词数
Set<Map.Entry<String,Double>> cateWordsNumSet = cateWordsNum.entrySet();
for(Iterator<Map.Entry<String,Double>> it = cateWordsNumSet.iterator(); it.hasNext();){
Map.Entry<String, Double> me = it.next();
totalWordsNum += me.getValue();
}
//下面开始读取测试样例做分类
Vector<String> testFileWords = new Vector<String>();
String word;
File[] testDirFiles = new File(testDir).listFiles();
FileWriter crWriter = new FileWriter(classifyResultFileNew);
for(int i = 0; i < testDirFiles.length; i++){
File[] testSample = testDirFiles[i].listFiles();
for(int j = 0;j < testSample.length; j++){
testFileWords.clear();
FileReader spReader = new FileReader(testSample[j]);
BufferedReader spBR = new BufferedReader(spReader);
while((word = spBR.readLine()) != null){
testFileWords.add(word);
}
//下面分别计算该测试样例属于二十个类别的概率
File[] trainDirFiles = new File(trainDir).listFiles();
BigDecimal maxP = new BigDecimal(0);
String bestCate = null;
for(int k = 0; k < trainDirFiles.length; k++){
BigDecimal p = computeCateProb(trainDirFiles[k], testFileWords, cateWordsNum, totalWordsNum, cateWordsProb);
if(k == 0){
maxP = p;
bestCate = trainDirFiles[k].getName();
continue;
}
if(p.compareTo(maxP) == 1){
maxP = p;
bestCate = trainDirFiles[k].getName();
}
}
crWriter.append(testSample[j].getName() + " " + bestCate + "\n");
crWriter.flush();
}
}
crWriter.close();
}
/**统计某类训练样本中每个单词的出现次数
* @param strDir 训练样本集目录
* @return Map<String,Double> cateWordsProb 用"类目_单词"对来索引的map,保存的val就是该类目下该单词的出现次数
* @throws IOException
*/
public Map<String,Double> getCateWordsProb(String strDir) throws IOException{
Map<String,Double> cateWordsProb = new TreeMap<String,Double>();
File sampleFile = new File(strDir);
File [] sampleDir = sampleFile.listFiles();
String word;
for(int i = 0;i < sampleDir.length; i++){
File [] sample = sampleDir[i].listFiles();
for(int j = 0; j < sample.length; j++){
FileReader samReader = new FileReader(sample[j]);
BufferedReader samBR = new BufferedReader(samReader);
while((word = samBR.readLine()) != null){
String key = sampleDir[i].getName() + "_" + word;
if(cateWordsProb.containsKey(key)){
double count = cateWordsProb.get(key) + 1.0;
cateWordsProb.put(key, count);
}
else {
cateWordsProb.put(key, 1.0);
}
}
}
}
return cateWordsProb;
}
/**计算某一个测试样本属于某个类别的概率
* @param Map<String, Double> cateWordsProb 记录每个目录中出现的单词及次数
* @param File trainFile 该类别所有的训练样本所在目录
* @param Vector<String> testFileWords 该测试样本中的所有词构成的容器
* @param double totalWordsNum 记录所有训练样本的单词总数
* @param Map<String, Double> cateWordsNum 记录每个类别的单词总数
* @return BigDecimal 返回该测试样本在该类别中的概率
* @throws Exception
* @throws IOException
*/
private BigDecimal computeCateProb(File trainFile, Vector<String> testFileWords, Map<String, Double> cateWordsNum, double totalWordsNum, Map<String, Double> cateWordsProb) throws Exception {
// TODO Auto-generated method stub
BigDecimal probability = new BigDecimal(1);
double wordNumInCate = cateWordsNum.get(trainFile.getName());
BigDecimal wordNumInCateBD = new BigDecimal(wordNumInCate);
BigDecimal totalWordsNumBD = new BigDecimal(totalWordsNum);
for(Iterator<String> it = testFileWords.iterator(); it.hasNext();){
String me = it.next();
String key = trainFile.getName()+"_"+me;
double testFileWordNumInCate;
if(cateWordsProb.containsKey(key)){
testFileWordNumInCate = cateWordsProb.get(key);
}else testFileWordNumInCate = 0.0;
BigDecimal testFileWordNumInCateBD = new BigDecimal(testFileWordNumInCate);
BigDecimal xcProb = (testFileWordNumInCateBD.add(new BigDecimal(0.0001))).divide(totalWordsNumBD.add(wordNumInCateBD),10, BigDecimal.ROUND_CEILING);
probability = probability.multiply(xcProb);
}
BigDecimal res = probability.multiply(wordNumInCateBD.divide(totalWordsNumBD,10, BigDecimal.ROUND_CEILING));
return res;
}
/**获得每个类目下的单词总数
* @param trainDir 训练文档集目录
* @return Map<String, Double> <目录名,单词总数>的map
* @throws IOException
*/
private Map<String, Double> getCateWordsNum(String trainDir) throws IOException {
// TODO Auto-generated method stub
Map<String,Double> cateWordsNum = new TreeMap<String,Double>();
File[] sampleDir = new File(trainDir).listFiles();
for(int i = 0; i < sampleDir.length; i++){
double count = 0;
File[] sample = sampleDir[i].listFiles();
for(int j = 0;j < sample.length; j++){
FileReader spReader = new FileReader(sample[j]);
BufferedReader spBR = new BufferedReader(spReader);
while(spBR.readLine() != null){
count++;
}
}
cateWordsNum.put(sampleDir[i].getName(), count);
}
return cateWordsNum;
}
/**根据正确类目文件和分类结果文件统计出准确率
* @param classifyResultFile 正确类目文件
* @param classifyResultFileNew 分类结果文件
* @return double 分类的准确率
* @throws IOException
*/
double computeAccuracy(String classifyResultFile,
String classifyResultFileNew) throws IOException {
// TODO Auto-generated method stub
Map<String,String> rightCate = new TreeMap<String,String>();
Map<String,String> resultCate = new TreeMap<String,String>();
rightCate = getMapFromResultFile(classifyResultFile);
resultCate = getMapFromResultFile(classifyResultFileNew);
Set<Map.Entry<String, String>> resCateSet = resultCate.entrySet();
double rightCount = 0.0;
for(Iterator<Map.Entry<String, String>> it = resCateSet.iterator(); it.hasNext();){
Map.Entry<String, String> me = it.next();
if(me.getValue().equals(rightCate.get(me.getKey()))){
rightCount ++;
}
}
computerConfusionMatrix(rightCate,resultCate);
return rightCount / resultCate.size();
}
/**根据正确类目文件和分类结果文计算混淆矩阵并且输出
* @param rightCate 正确类目对应map
* @param resultCate 分类结果对应map
* @return double 分类的准确率
* @throws IOException
*/
private void computerConfusionMatrix(Map<String, String> rightCate,
Map<String, String> resultCate) {
// TODO Auto-generated method stub
int[][] confusionMatrix = new int[20][20];
//首先求出类目对应的数组索引
SortedSet<String> cateNames = new TreeSet<String>();
Set<Map.Entry<String, String>> rightCateSet = rightCate.entrySet();
for(Iterator<Map.Entry<String, String>> it = rightCateSet.iterator(); it.hasNext();){
Map.Entry<String, String> me = it.next();
cateNames.add(me.getValue());
}
cateNames.add("rec.sport.baseball");//防止数少一个类目
String[] cateNamesArray = cateNames.toArray(new String[0]);
Map<String,Integer> cateNamesToIndex = new TreeMap<String,Integer>();
for(int i = 0; i < cateNamesArray.length; i++){
cateNamesToIndex.put(cateNamesArray[i],i);
}
for(Iterator<Map.Entry<String, String>> it = rightCateSet.iterator(); it.hasNext();){
Map.Entry<String, String> me = it.next();
confusionMatrix[cateNamesToIndex.get(me.getValue())][cateNamesToIndex.get(resultCate.get(me.getKey()))]++;
}
//输出混淆矩阵
double[] hangSum = new double[20];
System.out.print(" ");
for(int i = 0; i < 20; i++){
System.out.print(i + " ");
}
System.out.println();
for(int i = 0; i < 20; i++){
System.out.print(i + " ");
for(int j = 0; j < 20; j++){
System.out.print(confusionMatrix[i][j]+" ");
hangSum[i] += confusionMatrix[i][j];
}
System.out.println(confusionMatrix[i][i] / hangSum[i]);
}
System.out.println();
}
/**从分类结果文件中读取map
* @param classifyResultFileNew 类目文件
* @return Map<String, String> 由<文件名,类目名>保存的map
* @throws IOException
*/
private Map<String, String> getMapFromResultFile(
String classifyResultFileNew) throws IOException {
// TODO Auto-generated method stub
File crFile = new File(classifyResultFileNew);
FileReader crReader = new FileReader(crFile);
BufferedReader crBR = new BufferedReader(crReader);
Map<String, String> res = new TreeMap<String, String>();
String[] s;
String line;
while((line = crBR.readLine()) != null){
s = line.split(" ");
res.put(s[0], s[1]);
}
return res;
}
/**
* @param args
* @throws Exception
*/
public void NaiveBayesianClassifierMain(String[] args) throws Exception {
//TODO Auto-generated method stub
//首先创建训练集和测试集
CreateTrainAndTestSample ctt = new CreateTrainAndTestSample();
NaiveBayesianClassifier nbClassifier = new NaiveBayesianClassifier();
ctt.filterSpecialWords();//根据包含非特征词的文档集生成只包含特征词的文档集到processedSampleOnlySpecial目录下
double[] accuracyOfEveryExp = new double[10];
double accuracyAvg,sum = 0;
for(int i = 0; i < 10; i++){//用交叉验证法做十次分类实验,对准确率取平均值
String TrainDir = "F:/DataMiningSample/TrainSample"+i;
String TestDir = "F:/DataMiningSample/TestSample"+i;
String classifyRightCate = "F:/DataMiningSample/classifyRightCate"+i+".txt";
String classifyResultFileNew = "F:/DataMiningSample/classifyResultNew"+i+".txt";
ctt.createTestSamples("F:/DataMiningSample/processedSampleOnlySpecial", 0.9, i,classifyRightCate);
nbClassifier.doProcess(TrainDir,TestDir,classifyResultFileNew);
accuracyOfEveryExp[i] = nbClassifier.computeAccuracy (classifyRightCate, classifyResultFileNew);
System.out.println("The accuracy for Naive Bayesian Classifier in "+i+"th Exp is :" + accuracyOfEveryExp[i]);
}
for(int i = 0; i < 10; i++){
sum += accuracyOfEveryExp[i];
}
accuracyAvg = sum / 10;
System.out.println("The average accuracy for Naive Bayesian Classifier in all Exps is :" + accuracyAvg);
}
}
1 |
|
马尔可夫模型又可视为随机的有限状态机。马尔柯夫链可以表示成状态图(转移弧上有概率的非确定的有限状态自动机),如下图所示,
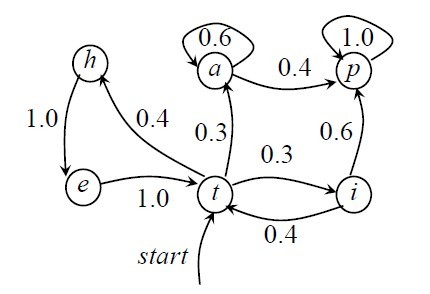
在上图中,圆圈表示状态,状态之间的转移用带箭头的弧表示,弧上的数字为状态转移的概率,初始状态用标记为start的输入箭头表示,假设任何状态都可作为终止状态。图中零概率的转移弧省略,且每个节点上所有发出弧的概率之和等于1。从上图可以看出,马尔可夫模型可以看做是一个转移弧上有概率的非确定的有限状态自动机。
3.2.2、隐马可夫模型(HMM)
在上文介绍的马可夫模型中,每个状态代表了一个可观察的事件,所以,马可夫模型有时又称作视马可夫模型(VMM),这在某种程度上限制了模型的适应性。而在我们的隐马可夫模型(HMM)中,我们不知道模型所经过的状态序列,只知道状态的概率函数,也就是说,观察到的事件是状态的随机函数,因此改模型是一个双重的随机过程。其中,模型的状态转换是不可观察的,即隐蔽的,可观察事件的随机过程是隐蔽的状态过程的随机函数。
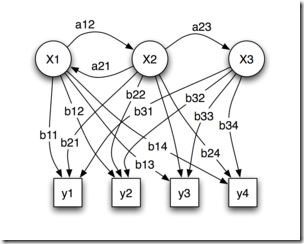
理论多说无益,接下来,再举个例子。N 个袋子,每个袋子中有M 种不同颜色的球。一实验员根据某一概率分布选择一个袋子,然后根据袋子中不同颜色球的概率分布随机取出一个球,并报告该球的颜色。对局外人:可观察的过程是不同颜色球的序列,而袋子的序列是不可观察的。每只袋子对应HMM中的一个状态,球的颜色对应于HMM 中状态的输出。
3.2.3、HMM在中文分词、机器翻译等方面的具体应用
隐马可夫模型在很多方面都有着具体的应用,如由于隐马可夫模型HMM提供了一个可以综合利用多种语言信息的统计框架,因此,我们完全可以讲汉语自动分词与词性标注统一考察,建立基于HMM的分词与词性标注的一体化系统。
根据上文对HMM的介绍,一个HMM通常可以看做由两部分组成:一个是状态转移模型,一个是状态到观察序列的生成模型。具体到中文分词这一问题中,可以把汉字串或句子S作为输入,单词串Sw为状态的输出,即观察序列,Sw=w1w2w3…wN(N>=1),词性序列St为状态序列,每个词性标记ct对应HMM中的一个状态qi,Sc=c1c2c3…cn。
那么,利用HMM处理问题问题恰好对应于解决HMM的三个基本问题:
- 估计模型的参数;
- 对于一个给定的输入S及其可能的输出序列Sw和模型u=(A,B,*),快速地计算P(Sw|u),所有可能的Sw中使概率P(Sw|u)最大的解就是要找的分词效果;
- 快速地选择最优的状态序列或词性序列,使其最好地解释观察序列。
除中文分词方面的应用之外,HMM还在统计机器翻译中有应用,如基于HMM的词对位模型,更多请参考:统计自然语言处理,宗成庆编著。
注:本文着重讲决策树分类和贝叶斯分类算法,后面的EM、HMM都是一笔带过,篇幅有限+懒,未能详尽阐述。日后,有机会,会再讲讲EM和HMM算法的。当然,你还可以先看看一个叫做HMM学习最佳范例的系列,原文写得好,翻译也翻译的精彩,推荐给大家:http://www.52nlp.cn/category/hidden-markov-model/page/4。
参考文献及推荐阅读
- 机器学习,Tom M.Mitchhell著;
- 数据挖掘导论,[美] Pang-Ning Tan / Michael Steinbach / Vipin Kumar 著;
- 数据挖掘领域十大经典算法初探;
- 数学之美番外篇:平凡而又神奇的贝叶斯方法(本文第二部分、贝叶斯分类主要来自此文);
- 从贝叶斯方法谈到贝叶斯网络;
- http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html;
- 数学之美:http://www.google.com.hk/ggblog/googlechinablog/2006/04/blog-post_2507.html;
- 决策树ID3分类算法的C++实现 & yangliuy:http://blog.csdn.net/yangliuy/article/details/7322015;
- yangliuy,http://blog.csdn.net/yangliuy/article/details/7400984;
- 统计自然语言处理,宗成庆编著(本文第三部分之HMM主要参考此书);
- 推荐引擎算法学习导论;
- 支持向量机导论,[美] Nello Cristianini / John Shawe-Taylor 著;
- Porter算法,http://qinxuye.me/article/porter-stemmer/;
- 漫谈Clustering之k-means:http://blog.pluskid.org/?p=17;
- HMM学习最佳范例:http://www.52nlp.cn/category/hidden-markov-model/page/4;
- 朴素贝叶斯新闻分类器详解:http://www.sobuhu.com/archives/610;
- 一堆 Wikipedia 条目,一堆 paper ,《机器学习与人工智能资源导引》。
后记
研究了一年有余的数据结构方面的算法,现在可以逐渐转向应用方面(机器学习 & 数据挖掘)的算法学习了。OK,本文或本聚类 & 分类算法系列中任何一篇文章有任何问题,漏洞,或bug,欢迎任何读者随时不吝赐教 & 指正,感谢大家,谢谢。
这些东西现在只是一个大致粗略的预览学习,以后若有机会,都会逐一更进一步深入(每一个分类方法或算法都足以写成一本书)。July、二零一二年五月二十八日晚十点。